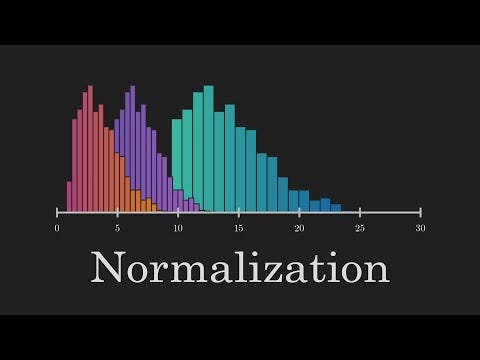
Introduction to Normalization in Machine Learning
In the realm of machine learning, data preprocessing is not just a preliminary step; it’s the foundation upon which successful models are built. Among all preprocessing techniques, normalization stands out as one of the most critical and frequently applied methods. Whether you’re building a simple linear regression or a complex ensemble model, understanding and properly implementing normalization can make the difference between model failure and outstanding performance.
What is Normalization?
Normalization is the process of scaling numerical data to a standard range or distribution, ensuring that all features (the individual measurable properties or characteristics of the data) contribute equally to the model’s learning process without any single feature dominating due to its inherent scale.
The Fundamental Problem
Consider a customer dataset containing:
- Age: 18-65 years
- Annual Income: $25,000-$150,000
- Purchase Frequency: 1-20 times per month
Without normalization, distance-based algorithms would assign 1000 times more weight to Annual income differences compared to purchase frequency, resulting in biased models.
Why Normalization is Essential in Machine Learning?
Machine learning models will perceive these features based on their raw numerical values. The massive difference in scales causes two major issues:
1. Problem for Distance-Based Algorithms (K-NN, K-Means, SVM)
Imagine we have two customers:
- Customer A: [Age=25, Income=$30,000, Frequency=15]
- Customer B: [Age=60, Income=$140,000, Frequency=5]
Let’s calculate the Euclidean Distance between them:
[ Distance = sqrt{(25-60)^2 + (30000-140000)^2 + (15-5)^2} ]
[ = sqrt{(-35)^2 + (-110,000)^2 + (10)^2} ]
[ = sqrt{1225 + 12,100,000,000 + 100} ]
[ approx sqrt{12,100,000,000} approx 110,000 ]
The distance is almost entirely determined by the income feature. The contributions from Age and Frequency are completely negligible.
2. Problem for Gradient-Based Algorithms (Linear/Logistic Regression, Neural Networks)
These models assign a weight to each feature during training. A small change in Income (e.g., +$1,000) leads to a large numerical change in the model’s output, while a large change in Purchase Frequency (e.g., +5 times/month) leads to a relatively small numerical change.
The Solution With Normalization
Let’s apply Standardization (a common normalization technique) which rescales data to have a mean of 0 and a standard deviation of 1. After standardization, the data would look something like this:
- Age: Values might range from approx. -1.5 to +1.5
- Annual Income: Values might range from approx. -1.5 to +1.5
- Purchase Frequency: Values might range from approx. -1.5 to +1.5
Now, let’s recalculate the distance between our two customers after standardization: - Customer A (Standardized): [Age=-0.8, Income=-1.3, Frequency=1.2]
- Customer B (Standardized): [Age=1.2, Income=1.4, Frequency=-0.7]
[ Distance = sqrt{(-0.8 – 1.2)^2 + (-1.3 – 1.4)^2 + (1.2 – (-0.7))^2} ]
[ = sqrt{(-2.0)^2 + (-2.7)^2 + (1.9)^2} ]
[ = sqrt{4 + 7.29 + 3.61} = sqrt{14.9} approx 3.86 ]
Now, all three features contribute meaningfully to the distance.
Conclusion
Normalization is not merely a technical step but a fundamental prerequisite for building robust and effective machine learning models. By transforming features onto a common scale, we ensure that each variable contributes equitably to the learning process, allowing the model to uncover the true underlying patterns in the data.
FAQs
Q: What is normalization in machine learning?
A: Normalization is the process of scaling numerical data to a standard range or distribution, ensuring that all features contribute equally to the model’s learning process.
Q: Why is normalization essential in machine learning?
A: Normalization prevents features with large ranges from dominating the model, allowing all features to contribute equally to the learning process.
Q: What are the common normalization techniques?
A: Common normalization techniques include Standardization, Min-Max Scaling, and Robust Scaling.
Q: How does normalization affect distance-based algorithms?
A: Normalization ensures that all features contribute equally to the distance calculation, preventing features with large ranges from dominating the distance.
Q: How does normalization affect gradient-based algorithms?
A: Normalization ensures that the model’s weights are updated efficiently and effectively, preventing features with large ranges from causing unstable training.