Introduction to the US Math Olympiad
The US Math Olympiad (USAMO) serves as a qualifier for the International Math Olympiad and presents a much higher bar than tests like the American Invitational Mathematics Examination (AIME). While AIME problems are difficult, they require integer answers. USAMO demands contestants write out complete mathematical proofs, scored for correctness, completeness, and clarity over nine hours and two days.
Evaluation of AI Reasoning Models
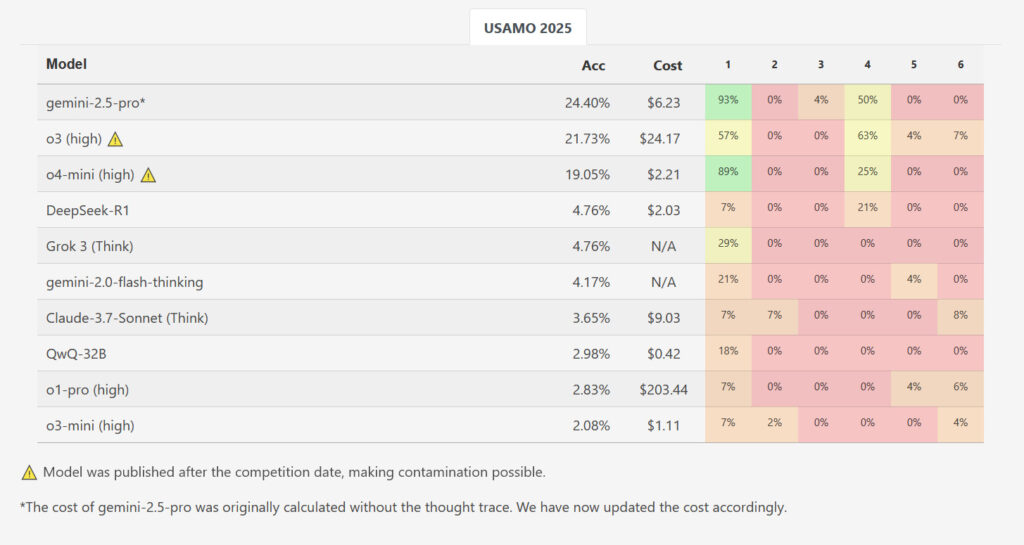
The researchers evaluated several AI reasoning models on the six problems from the 2025 USAMO shortly after their release, minimizing any chance the problems were part of the models’ training data. These models included Qwen’s QwQ-32B, DeepSeek R1, Google’s Gemini 2.0 Flash Thinking (Experimental) and Gemini 2.5 Pro, OpenAI’s o1-pro and o3-mini-high, Anthropic’s Claude 3.7 Sonnet with Extended Thinking, and xAI’s Grok 3.
Performance of AI Models
While one model, Google’s Gemini 2.5 Pro, achieved a higher average score of 10.1 out of 42 points (~24 percent), the results otherwise showed a massive performance drop compared to AIME-level benchmarks. The other evaluated models lagged considerably further behind: DeepSeek R1 and Grok 3 averaged 2.0 points each, Google’s Flash-Thinking scored 1.8, Anthropic’s Claude 3.7 managed 1.5, while Qwen’s QwQ and OpenAI’s o1-pro both averaged 1.2 points. OpenAI’s o3-mini had the lowest average score at just 0.9 points (~2.1 percent). Out of nearly 200 generated solutions across all tested models and runs, not a single one received a perfect score for any problem.
How the Models Failed
In the paper, the researchers identified several key recurring failure patterns. The AI outputs contained logical gaps where mathematical justification was lacking, included arguments based on unproven assumptions, and continued producing incorrect approaches despite generating contradictory results.
A specific example involved USAMO 2025 Problem 5. This problem asked models to find all positive whole numbers “k,” such that a specific calculation involving sums of binomial coefficients raised to the power of “k” would always result in an integer, no matter which positive integer “n” was used. On this problem, Qwen’s QwQ model made a notable error: It incorrectly excluded non-integer possibilities at a stage where the problem statement allowed them. This mistake led the model to an incorrect final answer despite having correctly identified the necessary conditions earlier in its reasoning process.
Conclusion
The results of the study show that current AI models still have a long way to go in terms of mathematical reasoning and problem-solving. While they may perform well on certain types of problems, they struggle with more complex and abstract mathematical concepts. Further research and development are needed to improve the performance of AI models in mathematical reasoning and problem-solving.
Frequently Asked Questions
What is the US Math Olympiad?
The US Math Olympiad (USAMO) is a mathematics competition for high school students in the United States. It is a qualifier for the International Math Olympiad and requires contestants to write out complete mathematical proofs, scored for correctness, completeness, and clarity.
What were the results of the study?
The study found that current AI models performed poorly on the USAMO problems, with the best model achieving a score of 24% and the worst model achieving a score of 2.1%. The models struggled with logical gaps, unproven assumptions, and incorrect approaches.
What are the implications of the study?
The study highlights the limitations of current AI models in mathematical reasoning and problem-solving. It suggests that further research and development are needed to improve the performance of AI models in these areas.











