Introduction to Computer Numbers
During day-to-day programming or general computer use, it’s common to overlook how the computer handles numbers in its definition. But this easily becomes a problem when we try to optimize a solution and even in unavoidable situations.
What Really is the Danger
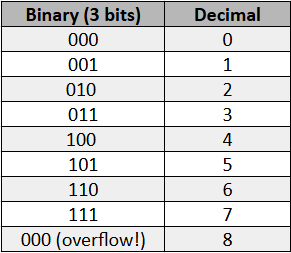
Computers represent numbers using bits, their most basic binary unit. Each memory has a bit storage capacity defined by current technology, so if we have a computer that operates with 3 bits, we have the following situation:
When we add 1 when we’re at the maximum number of bits, we encounter a problem since we would need 1 more bit to represent that number. In computing, this is called an integer overflow. When a sum results in integers that are too large for the chosen type, the result “turns inside out."
For example, in Python:
import numpy as np
# Define the largest 32-bit signed integer
x = np.int32(2147483647)
print("Before overflow:", x)
# Add 1 -> causes overflow
x = x + np.int32(1)
print("After overflow:", x)Output:
Before overflow: 2147483647
After overflow: -2147483648This behavior isn’t a bug, but rather a consequence of the limits of binary representation. In several famous examples, this occurs with real-world problems.
Unexpected Famous Cases
The Boeing 787 Case (2015)
In 2015, Boeing discovered that the Boeing 787 Dreamliner’s generators could shut down mid-flight if they were left on for 248 consecutive days without being restarted.
The reason? An internal timer, based on 32-bit integers, would overflow after this period, leading to a failure in the aircraft’s power management.
The fix was simple: Periodically restart the system to reset the count and memory to zero, but the potential impact was enormous.
The Level 256 Bug in Pac-Man
Those who played Pac-Man in the arcades may be familiar with the “Kill Screen.” After level 255, the level counter (stored in 8 bits) overflows upon reaching 256. This creates a glitched screen, with half the maze unreadable, making the game impossible to complete.
The developers didn’t expect anyone to play 256 levels of Pac-Man, so they didn’t handle this exception!
The Bug of 2038
In the past, just before the year 2000, the bug of the millennium event was very popular: it said that many computers could have a bug due to the change of year 31/12/99 to 01/01/00 after midnight. Gladly, everything turned out fine, but now another catastrophic event looms just like a new Maya prophecy.
Many Unix and C systems use a signed 32-bit integer to count seconds since January 1, 1970 (the famous Unix timestamp). This counter will reach its limit on January 19, 2038, overflowing around 2.147.483.647 seconds. If left unfixed, any software that relies on time could exhibit unpredictable behavior.
How Float Variables Work
Floats (floating-point numbers) are used to represent real numbers in computers, but unlike integers, they cannot represent every value exactly. Instead, they store numbers approximately using a sign, exponent, and mantissa (according to the IEEE 754 standard).
And just like the integers of previous examples, the mantissa and exponent are represented by bits that are finite. Its value will depend on the number of bits such as 16, 32 or 64 defined by the variable declaration.
Float16, Float32, and Float64
- Float16 (16 bits): Can represent values roughly from 6.1 × 10⁻⁵ to 6.5 × 10⁴, precision of about 3–4 decimal digits, uses 2 bytes (16 bits) of memory
- Float32 (32 bits): Can represent values roughly from 1.4 × 10⁻⁴⁵ to 3.4 × 10³⁸, precision of about 7 decimal digits, uses 4 bytes of memory
- Float64 (64 bits): Can represent values roughly from 5 × 10⁻³²⁴ to 1.8 × 10³⁰⁸, precision of about 16 decimal digits, uses 8 bytes of memory
The Trade-Offs Applied in Machine Learning
The higher precision of float64 uses twice the memory and can be slower than float32 and float16, but is it necessary to use float64?
Deep learning models can have hundreds of millions of parameters. Using float64 would double the memory consumption. For many ML models, including neural networks, float32 is sufficient and allows faster computation with lower memory usage. Some are even studying the application of float16.
In theory, always using the highest precision type seems safe, but in practice Modern GPUs (RTX, for example) perform poorly on float64, while they are optimized for float32 and in some cases float16. For example, float64 are 10–30x slower on GPUs optimized for float32.
Benchmarks
A simple benchmark test can be made by multiplying matrix:
import numpy as np
import time
# Matrix size
N = 500
# Matrix with different float bit sizes
A32 = np.random.rand(N, N).astype(np.float32)
B32 = np.random.rand(N, N).astype(np.float32)
A64 = A32.astype(np.float64)
B64 = B32.astype(np.float64)
A16 = A32.astype(np.float16)
B16 = B32.astype(np.float16)
def benchmark(A, B, dtype_name):
start = time.time()
C = A @ B # multiply matrix
end = time.time()
print(f"{dtype_name}: {end - start:.5f} seconds")
benchmark(A16, B16, "float16")
benchmark(A32, B32, "float32")
benchmark(A64, B64, "float64")Example of output (it will depend on computational resources):
float16: 0.01 seconds
float32: 0.02 seconds
float64: 0.15 secondsThat said, an important point is that common problems in Machine Learning model performances, such as gradients, are not solved simply by increasing accuracy, but rather by making good architectural choices.
Good Practices to Solve It
In deep networks, gradients can become very small after traversing several layers. In float32, values smaller than ~1e-45 literally become zero.
This means that the weights are no longer updated — the infamous vanishing gradient problem.
But the solution isn’t to migrate to float64. Instead, we have smarter solutions.
ReLU
Unlike sigmoid and tanh, which flatten values and make the gradient disappear, ReLU keeps the derivative equal to 1 for x > 0.
This prevents the gradient from reaching zero too quickly.
Batch Normalization
Normalizes the activations in each batch to keep means close to 0 and variances close to 1. This way, the values remain within the safe range of float32 representation.
Residual Connections (ResNet)
They create “shortcuts” through a specific function so the gradient can span multiple layers without disappearing. They allow networks with 100+ layers to work well in float32.
Conclusion
In conclusion, the way computers handle numbers can lead to problems such as integer overflow and floating-point precision issues. These problems can have significant consequences, as seen in famous cases such as the Boeing 787 and Pac-Man. However, by understanding how computers represent numbers and using good practices such as ReLU, batch normalization, and residual connections, we can mitigate these issues and build more robust machine learning models.
FAQs
Q: What is integer overflow?
A: Integer overflow occurs when a sum results in integers that are too large for the chosen type, causing the result to "turn inside out."
Q: What is the difference between float16, float32, and float64?
A: The main difference is the number of bits used to represent the number, which affects the precision and range of values that can be represented.
Q: Why is float32 sufficient for many ML models?
A: Float32 is sufficient because it provides a good balance between precision and memory usage, and many ML models do not require the higher precision of float64.
Q: What is the vanishing gradient problem?
A: The vanishing gradient problem occurs when gradients become very small after traversing several layers, causing the weights to no longer be updated.
Q: How can we mitigate the vanishing gradient problem?
A: We can mitigate the vanishing gradient problem by using techniques such as ReLU, batch normalization, and residual connections.